静電気とは

静電気の発生現象

静電気は、電気的に中性な材質の異なる2つの物体を接触させて、分離すると発生します。

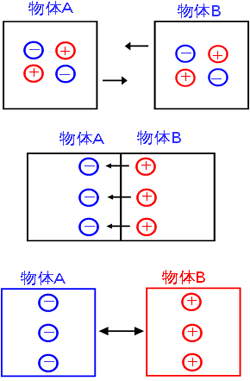
(1)物体A、Bの接触
電気的に中性(プラスとマイナスの電荷が等量)な物体A、B

(2)電荷の移動
金属同士の接触では、仕事関数が小さい方から大きい方へ電子が移動する。すなわち、仕事関数が小さい方はプラスに、仕事関数が大きい方はマイナスに帯電することになる。

(3)物体A、Bの分離
物体Aはマイナスに、物体Bはプラスに帯電する。

図1.接触帯電による静電気の発生

静電気は、固体-固体、固体-液体、液体-液体の組み合わせでも、物体同士を接触した後、分離することで発生します。その事例を図2に示します。

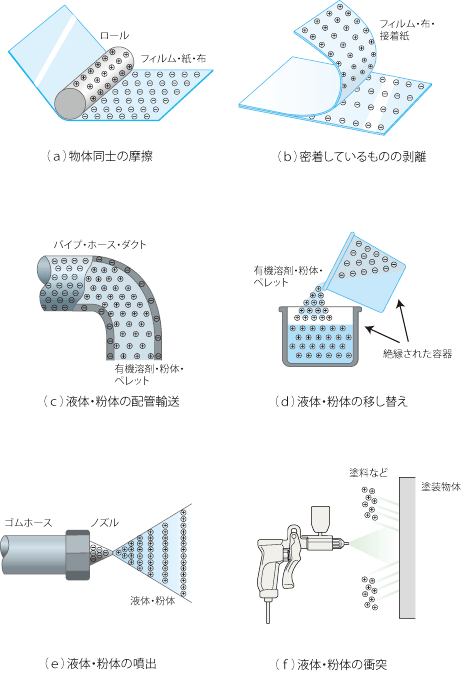
図2.静電気の発生事例

いずれの静電気発生現象でも、2つの物体間では、接触し、分離する過程が存在します。

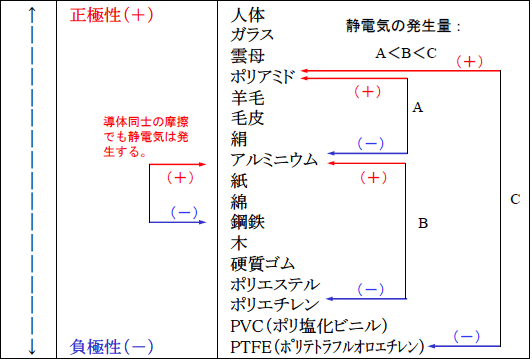
図3.帯電列

帯電列にある2つの物体を摩擦すると、帯電列の上の位置にある物が正極性に、下の位置にあるものが負極性帯電します。また、帯電列中での位置が離れている2つの物体(C)の方が、位置が近い(B)、より近い(A)の物体よりも、静電気の発生量が大きくなる(A<B<C)。さらに、帯電列中には、導体も含まれており、導体も絶縁されている状態では、導体同士を摩擦すると静電気が発生し、帯電することに留意する必要があります。

物体が帯電すると

物体に静電気が帯電すると、図4に示すように帯電物体の周囲には、電界が発生します。

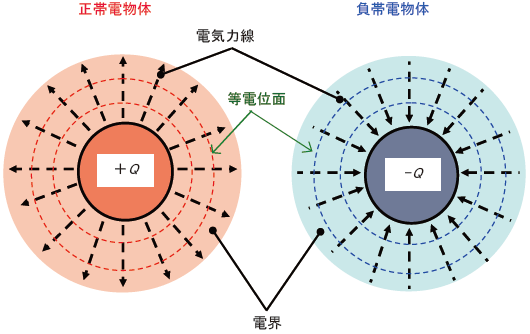
図4.帯電物体の周囲に発生する電界

電界とは、電荷に電気力(クーロン力)を作用させる性質を持つ空間のことで、電界が、時間および空間に対して変化しない場合を静電界と呼びます。電気力線は、ある点の単位面積を通過する電気力線の本数(電気力線の密度)が電界の強さを表し、その点での電気力線の接線方向が電界の方向を表します。また、電気力線は下記の性質を持っています。

• 1.電気力線は、正電荷から出て負電荷に終端する。
• 2.電気力線同士は交差しない。
• 3.電気力線は分岐しない。
• 4.電気力線が密な部分は、電界が強い。
• 5.電気力線が平行な部分は、平等電界である。
• 6.電気力線は、導体表面から垂直に出る(入る)。

図5は、2つの帯電物体間に形成される電気力線を示した一例です。

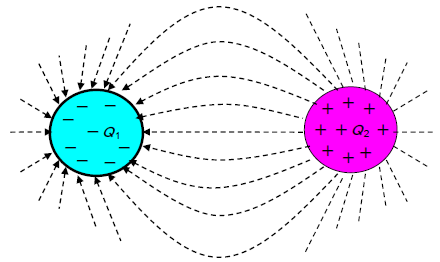
(a) 異符号間の電気力線

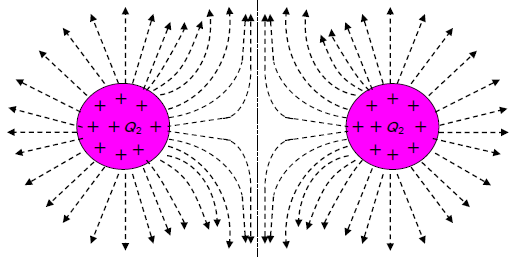
(b) 同極性間の電気力線

図5.2つの帯電物体間に形成される電気力線

ただし、電気力線は、電界を可視化するために考えられた架空の線ですが、電気力線を用いると2つの帯電物体間に形成される電界の様子がわかり、目に見えない静電気を考えやすくなります。例えば、図6は、帯電量の異なる2つの帯電物体の電気力線です。帯電物体Aの電荷量Q1と帯電物体Bの電荷量Q2がQ1<Q2の関係があるときの電気力線を表しています。帯電物体の大きさは同じなので、単位表面積当たりの電気力線数は、帯電物体Bに比べて帯電物体Aの方が少なくなり、電界強度はE1<E2になります。

E1:導体表面の電界強度

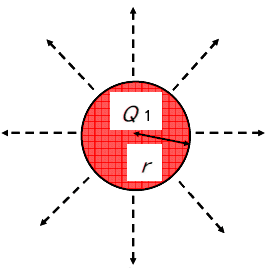
電気力線の密度:小 → 電界弱い

帯電導体球A

E2:導体表面の電界強度

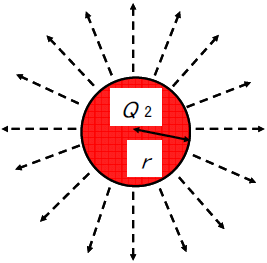
電気力線の密度:大 → 電界強い

帯電導体球B

図6.帯電量の異なる2つの帯電導体からでる電気力線

静電気力(クーロン力)とは

静電気力(クーロン力)は、静電気現象の源です。静電気力は、図7に示すように、2つの帯電物体の極性が異極性の場合と同極性の場合では、帯電物体間に働く力の向きが異なります。異極性の場合は引力(a)となり、同極性の場合は斥力(b)となります。

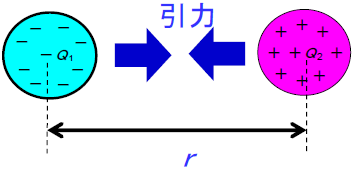
(a)異極性電荷間の力

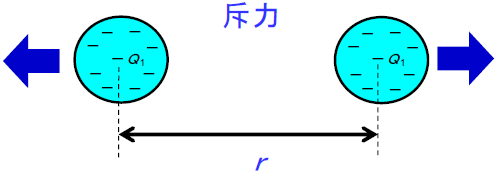
(b)同極性電荷間の力

図7.2つの帯電物体間に働く静電気力

また、静電気力(クーロン力)の強さは、(1)式に示すように2つの帯電物体の電荷量の積に比例し、帯電物体間の距離の2乗に反比例します。

F∝Q1・Q2/r²・・・・・・・・・・・・(1)

静電誘導現象も静電気力に起因する!!

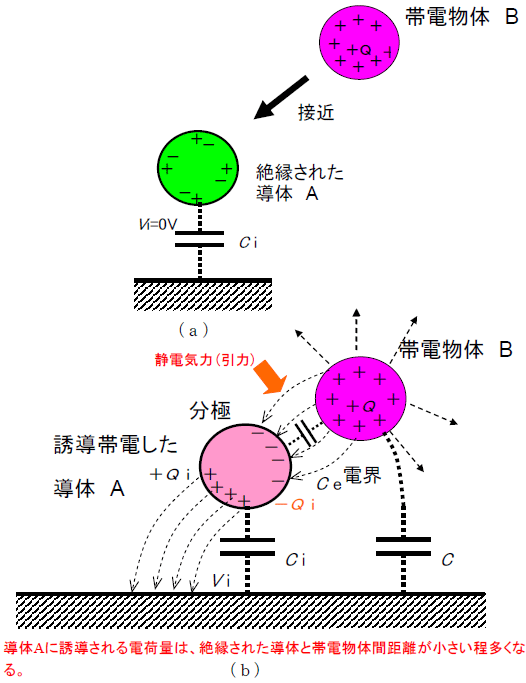
図8.静電気力に起因した静電誘導現象

静電気放電も静電気力(クーロン力)に起因します!!

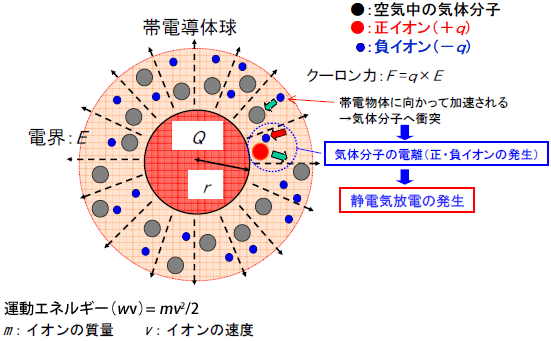
図9.静電気力に起因した静電気放電の発生

帯電物体の周囲の電界により、電界中に在る負イオン(電子)が静電気力(クーロン力)によって加速され、運動エネルギー(wv)を持つようになります。この負イオンが電界中にある気体分子に衝突したとき、下記の式が成り立つと、

気体分子の電離エネルギー<負イオンの運動エネルギー(wv)・・・(2)

気体分子から電子が弾き出されて、負イオンと正イオンが生成されます。ここで生じた負イオンに静電気力が作用し、負イオンが電界中で加速されて運動エネルギが(2)式の条件を満足すると、気体分子の電離が発生します。この過程が繰り返し起こることにより、静電気放電が発生することになります。

導体の電荷分布も静電気力(クーロン力)が影響します!!

1)電気的に中性な導体に電荷を与えると、与えられた電荷は導体の表面に分布します。すなわち、与えられた電荷は導体内部には存在しません。
これは、図10に示すように導体に負極性の電荷を4つ与えて、導体を負極性に帯電させせた場合を考えます。この時、4つの負極性電荷を導体内部に与えたとします(a)。4つの負極性電荷間には、静電気力(斥力)が働き、4つの電荷は、導体の表面に分布するようになります。

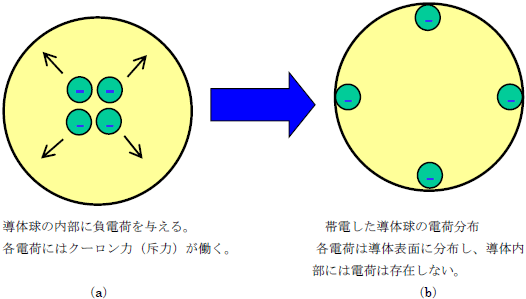
図10.帯電した導体球の電荷分布

2)電気的に中性な導体に電荷を与えると、前項で述べたように与えられた電荷は導体の表面に分布します。さらに、電荷は導体表面の電位が等電位になるように分布します。すなわち、与えられた電荷は導体内部には存在しません。導体電荷は、導体表面が等電位面になるように分布する。

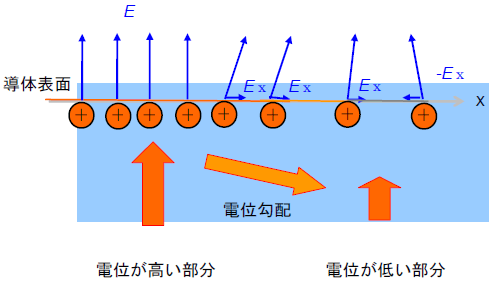
(a)導体表面に電位分布がある場合

導体表面に電位分布がある(a)と、導体表面に沿った電位勾配(電界Ex)が発生します。導体表面の電荷は、この電界Exによって表面に沿って電位が低い部分に移動して、低い部分の電位を高くします。電荷の移動は、導体表面の電位が等電位になるまで続きます。
その結果、導体表面から出る(に入る)電界は導体表面と垂直になります(b)

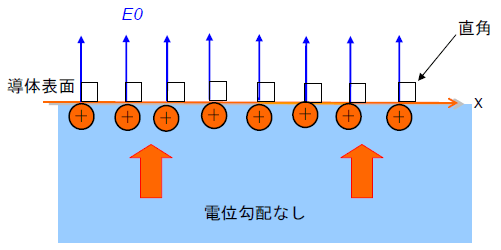
(b)導体表面が等電位になるように電荷が分布した場合

図11.導体表面の電荷分布は表面電位が等電位になるように分布します。

静電気トラブル事例

図12.静電気トラブルの一例